青海省干旱指数时空变化特征与气候指数的关系

引用本文

张世虎, 王一峰, 侯勤正, 董小刚, 孙坤. 青海省干旱指数时空变化特征与气候指数的关系. 草业科学, 2015,32(12):1980-1987
ZHANG Shi-hu, WANG Yi-feng, HOU Qin-zheng, DONG Xiao-gang, SUN Kun. Spatial and temporal characteristics of aridity index and association with AO and ENSO in Qinghai Province. Pratacultural Science,2015,32(12): 1980-1987 复制到剪切板

Permissions

《草业科学》编辑部

青海省干旱指数时空变化特征与气候指数的关系

张世虎¹, 王一峰¹, 侯勤正¹, 董小刚², 孙坤¹

1.西北师范大学生命科学学院,甘肃兰州 730070

2.西北师范大学地理与环境科学学院,甘肃兰州 730070

通讯作者:孙坤(1965-),男,甘肃民勤人,教授,博士,主要从事植物系统进化和生物多样性等方面的研究。E-mail:[email protected]

第一作者:张世虎(1980-),男,甘肃靖远人,讲师,博士,主要从事高寒生态系统生态学研究。E-mail:[email protected]

收稿日期: 2015-11-15

基金: 西北师范大学青年教师科研能力提升计划项目(NWNU-LKQN-14-12)

摘要

基于青海省29个气象台站1961-2013年的实测气象数据,应用Penman-Monteith模型、气候倾向率、空间分析、交叉小波和相干小波变换等方法分析青海省干旱指数的时空变化、影响因素及其与北极涛动(AO)和厄尔尼诺-南方涛动(ENSO)等气候指数的相互关系。结果表明,近53年来,青海省多年平均干旱指数为0.49,整体呈现出波动降低趋势,其线性降低速率为-0.03·10 a^-1 (α=0.01),表明青海省气候有变湿的趋势。研究区年内干旱指数呈现出先减小后增加的趋势,最小值出现在8月,最大值出现在12月。最高值出现在西北部的茫崖镇与中北部的格尔木市和诺木洪乡,最低值出现在中南部的曲麻莱县和东南部的久治县。青海省干旱指数与日照时数( P<0.01)和风速( P<0.05)总体呈现显著的正相关关系,而与温度和降水呈显著负相关关系( P<0.05)。此外,研究区干旱指数与北极涛动(AO)和厄尔尼诺-南方涛动(ENSO)指数存在多尺度的显著相关性( a=0.05)。

关键词: 潜在蒸散量; 干旱指数; 北极涛动; 厄尔尼诺-南方涛动; 青海省

中图分类号:S162.1 文献标志码:A 文章编号:1001-0629(2015)12-1980-08 doi: 10.11829/j.issn.1001-0629.2015-0543

Spatial and temporal characteristics of aridity index and association with AO and ENSO in Qinghai Province

ZHANG Shi-hu¹, WANG Yi-feng¹, HOU Qin-zheng¹, DONG Xiao-gang², SUN Kun¹

1.College of Life Science, Northwest Normal University, Lanzhou 730070, China

2.College of Geography and Environment Science, Northwest Normal University, Lanzhou 730070, China

Corresponding author: SUN Kun E-mail:[email protected]

Abstract

This study were used the methods of climate tendency rate, spatial analysis, Penman-Monteith model, the temporal-spatial variations, cross wavelet and wavelet coherence to analyze the spatial and temporal variations of AI (aridity index), influencing factors, and the relationship of the AI with AO (Arctic Oscillation) and ENSO (El Nino-Southern Oscillation), based on the data of 29 meteorological stations in Qinghai Province during the period of 1961-2013. The results showed that the average of AI was 0.49 for many years. The trend of AI fluctuantly reduced in the past 53 years. The average of AI linearly decreased at the rate of -0.03·10 a^-1 (α=0.01) over the study area, which means the climate gradually changes to moist in Qinghai Province. The maximum value and minimum value of AI appeared in December and August, respectively, which showed that the average of AI increased firstly then reduced within a year. The maximum of the AI appeared in northwest of Mangai County and north-central of Golmud City and Nuomuhong Town, and the minimum of AI appeared in southern-central of Maqulai County and Jiuzhi County. The average of AI had significantly positive correlation to sunshine time ( P<0.01) and wind velocity ( P<0.05) in Qinghai Province. At the same time,the average of AI has negative correlation with the temperature, precipitation and relative humidity. In addition, the average of AI is multi-scale significant correlation to AO and ENS in this study ( a=0.05).

Keyword: potential evapotranspiration; aridity index; arctic oscillation; el nino-southern oscillation; Qinghai Province

Show Figures

IPCC第五次报告表明:1880-2012年间全球平均温度升高0.85 ℃(0.65~1.06 ℃), 近乎全球都经历了升温过程; 在北半球, 1983-2012年可能是最近1 400 年来气温最高的30年^[1]。持续的全球变暖将影响全球和区域水循环的各个环节, 除通过降水和气温变化影响流域径流外, 还通过不同的方式对蒸散量产生了重要影响^[2]。因此, 在全球变暖背景下, 部分地区极端气候事件(例如暴雨、干旱等)发生的频率加快、强度增大, 且旱灾影响范围广, 造成了严重的经济损失。中国是世界上主要的干旱国家之一, 干旱半干旱区面积占全国土地面积的50%以上, 且主要集中在中国北方地区^{[3, 4]}。干旱事件及其影响程度大小的分析和评价需要一定的量化标准^[3], 但由于干旱是一种非常复杂的气象现象, 对其出现和持续时间与下垫面的状况密切相关, 至今对干旱的定义与强度没有一个统一的标准^{[3, 4, 5]}。干旱指数(Aridity Index, AI)是判断气候变化的重要指标, 它以同期潜在蒸散量和降水量的差再与潜在蒸散量的比值来表示^{[6, 7]}, 并以此来表示地表的干湿状况。青海省位于青藏高原东北部, 其气候具有高原特色, 主要以高寒干旱气候为主, 年均气温低(-5.7~8.5 ℃), 是典型的大陆性高原气候, 为我国气候变化较为敏感的区域之一^{[6, 8]}。此外, 由于受地形影响, 降水量比同纬度的东部地区少, 年降水量在50~450 mm; 年均风速达5.1 m· s^-1, 太阳辐射强, 年日照时数超过2 500 h, 是中国总辐射最大的省份之一^[7]。近年来, 结合气温和降水等指标对青藏高原及青海的气候特征研究相对较多, 已有的研究结果表明, 该区气候有明显的增暖增湿趋势^{[9, 10, 11, 12, 13, 14, 15]}。本研究选取AI指标对青海省地表干湿状况进行分析, 并深入研究其与北极涛动(AO)指数和厄尔尼诺-南方涛动(ENSO)指数的相互关系, 旨在从空间尺度上揭示全球气候变化对青海省干旱程度的影响, 深入了解该区域气候干湿变化的机理和水资源供需状态, 为该区生态环境建设与恢复、水资源合理利用以及资源可持续发展提供理论依据。

1 数据来源和研究方法

1.1 数据来源

选择青海省境内29个气象站点(图1)1961-2013年数据, 包括逐日平均气温、最高、最低气温、平均风速、平均相对湿度和日照时数等, 并以此数据为基础, 计算潜在蒸散量, 用潜在蒸散量和同期降水量的差值与潜在蒸散量的比值表示干旱指数。资料源自于国家气象信息中心(http://www.nmic.gov.cn/)。月平均北极涛动(AO)指数序列来源于NOAA网站(http://www.cpc.noaa.gov); 厄尔尼诺-南方涛动(ENSO)指数采用多元 ENSO 指数^[16](即MEI)替代, 数据来源于http://www.esrl.noaa.gov/psd/enso/mei/。

	Figure Option View Download New Window
	图1 研究区所选气象站点分布图Fig.1 The distribution of meteorological stations in Qinghai Province

1.2 研究方法

1.2.1 潜在蒸散量潜在蒸散量(ET₀)的计算采用 FAO 在1998 年推荐并修订的Penman-Monteith模型(简称P-M模型)^[17]:

ET₀= $\begin{matrix} \frac{0.408 Δ (R_{n} - G) + γ \frac{900}{T + 273} U_{2} (e_{s} - e_{a})}{Δ + γ (1 + 0.34 U_{2})} \end{matrix}$ (1)

式中, R_n为净辐射, Δ 为水汽压对温度的斜率(kPa· ℃^-1), G为土壤热通量(MJ· m^-2· d^-1, 本文忽略不计), γ 为干湿常数, U₂为2 m高处风速(m· s^-1), e_s为饱和水汽压(kPa), e_a为实际水汽压(kPa); T为平均气温(℃)。

1.2.2 干旱指数的计算采用Thornthwaite对干旱指数的定义方法, 此方法适用于干旱半干旱区; 利用同期潜在蒸散量和降水量的差值, 再与潜在蒸散量的比值来表示干旱指数^[8], 计算公式如下:

AI=(ET₀-P_r)/ET₀(2)

式中, AI是干旱指数; P_r是降水量(mm), ET₀是潜在蒸散量(mm)。若P_r小于且不等于ET₀, 则表示干旱; 若降水量为0, AI等于1, 表示该区域干旱程度最强; 若P_r等于或高于ET₀, 则AI等于0或者是负值, 表示此时干旱程度较低。

为进一步探究影响干旱指数下降的主要气象因子及其影响程度, 本研究采用多元回归方法, 分析了各气象因子:平均气温(T_mea)、降水(P_r)、日照时数(S_h)、相对湿度(R_h)和平均风速(U)等, 对干旱指数变化的影响, 并判断各气象因子对干旱指数变化的相对贡献率, 以此来确定各气象因子对干旱指数的影响程度。

1.2.3 交叉小波和小波相干交叉小波是将小波变换和交叉谱分析两种方法相结合而产生的一种信号分析手段^{[18, 19]}。该方法不仅可以从多时间尺度上来研究两个时间序列在时频域中的相互关系, 而且可以揭示两个序列在不同时段尺度上的一致性和相关性, 也能再现该时频域空间中的相位关系。本研究所采用的计算过程参考文献[18-20]的计算方法和程序:

交叉小波变换(XWT)是将两个时间序列X_n和Y_n 定义为:W^XY=W^XW^Y*, 其中* 为复共轭, 交叉小波谱定义为|W^XY|, 而两个时间序列X_n和Y_n的背景功率谱 $\begin{matrix} P_{k}^{x} \end{matrix}$ 和 $\begin{matrix} P_{k}^{y} \end{matrix}$ 则定义为:

$D [\begin{matrix} \frac{| W_{n}^{x} (S) W_{n}^{Y*} (S) |}{σXσY} \end{matrix} < p] = \begin{matrix} \frac{Z_{v} (p)}{v} \end{matrix} \begin{matrix} \sqrt[]{P_{k}^{X} P_{k}^{Y}} \end{matrix}$ (3)

式中, Z_v(p)为概率P的置信度水平, 源于两个χ ²分部小波谱乘积的平方根。

交叉小波的相位角定义为:

α _m=arg(X, Y)=arg[ $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ cos(a_i), $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ sin(a_i)] (4)

小波相位角的标准偏差为:

$s = \begin{matrix} \sqrt[]{- 2 \ln (R / n)} \end{matrix} = \begin{matrix} \sqrt[]{- 2 \ln (\sqrt[]{X^{2} + Y^{2}}) / n} \end{matrix}$ (5)

两列时间序列的小波相干谱也可以反映时频空间局部的相关性大小。定义为:

$\begin{matrix} R_{n}^{2} \end{matrix}$ (s)= $\begin{matrix} \frac{| S [s^{- 1} W_{n}^{XY} (s)] |^{2}}{S [s^{- 1} | W_{n}^{X} (s) |^{2}] \cdot S [s^{- 1} | W_{n}^{Y} (s) |^{2}]} \end{matrix}$ (6)

式中, S为平滑窗口, 定义为:

S(W)=S_scale{S_time[W_n(s)]}(7)

式中, S_scale为小波坐标尺度的平滑, S_time为时间尺度的平滑。

Morlet小波的平滑窗口定义为:

S_time(W)|s=(W_n(s)^* $\begin{matrix} {c_{1}}^{\frac{- t^{2}}{2 S^{2}}} \end{matrix}$ |(8)

S_scale(W)|s=W_n(s)^*c₂)∏ (0.6s)|_n(9)

式中, c₁和c₂是标准化常量, * 为复共轭, ∏ 为矩阵函数。

2 结果与分析

2.1 干旱指数的时间变化特征分析

在整个研究时段内青海省多年平均干旱指数为0.49, 整体呈现出波动降低趋势, 其线性降低速率为-0.03· 10 a^-1 (α =0.01), 表明青海省气候有变湿的趋势。其干旱指数的变幅在0.31~0.63, 其中干旱指数最大值出现在1962年, 为0.63, 而最小值出现在1989年, 为0.31(图2a)。干旱指数从20世纪60年代的0.56降低到90年代的0.44, 90年代之后降低趋势变缓, 20世纪90年代到2013年, 其值从0.44降低到0.42。

	Figure Option View Download New Window
	图2 青海省1961-2013年干旱指数年际变化(a)和年内变化(b)Fig.2 Change of annual (a) and monthly (b) average aridity index in Qinghai from 1961 to 2013

近53年来, 青海省月干旱指数有明显的变化趋势, 各月份之间表现为先降低后增加的趋势, 呈波谷状变化(图2b)。12月出现最大值(0.93), 8月出现最小值(-0.45)。AI指数冬季最大, 春季和秋季次之, 夏季最小, 表明青海省夏季气候湿润, 冬季较为干旱。

2.2 干旱指数的空间变化特征分析

以各个站点干旱指数的变化趋势系数为参数, 绘制青海省干旱指数的空间分布图(图3)。青海省各代表站点的干旱指数均呈下降趋势, 其中有16个站点的干旱指数变化趋势通过P< 0.01的显著性检验。青海省干旱指数变化趋势小于-0.3的站点主要集中在中部地区, 而变化趋势介于0~-0.3之间的站点散点式分布于整个研究区。究其原因主要是青海省西北部地区受西伯利亚冷高压影响显著, 多为干旱半干旱区, 降水较少, 干旱指数变化较大^[21]; 东北部主要受季风影响, 降水相对丰富, 干旱指数的变化相对较小; 南部主要受来自孟加拉湾暖湿气流影响, 降水最多, 干旱指数在整个研究区变化也较大。此外, 由于干旱指数受较多气象因子(例如:降水、气温等)的影响, 所以研究区干旱指数的空间分布也呈现出一定的空间差异性。

	Figure Option View Download New Window
	图3 1961-2013年青海省干旱指数变化趋势的空间分布Fig.3 Spatial distribution of the trend for AI in Qinghai from 1961 to 2013

2.3 气候因素对干旱指数的影响分析

青海省干旱指数主要与日照时数和风速总体呈现显著的正相关关系, 其相关系数分别为0.436(P< 0.01)和0.324(P< 0.05); 而与气温和降水等呈显著负相关关系(P< 0.05)。日照时数是影响青海省干旱指数变化的主要因素, 其次是降水和风速, 相对湿度对该区域的干旱指数的影响相对较小; 这与Huo等^[22]和Zhang等^[23]的研究结果较为相似。此外, 青海省近53年来除了气温升高和降水量增加外, 其余因素(日照时数、相对湿度和平均风速)均呈下降趋势, 且降水的增加值远大于潜在蒸散量的减少值。干旱指数变化与降水所需的气象条件相反, 即降水量越多, 云层越厚, 光照强度就越弱, 空气湿度就会增加, 这将会引起潜在蒸散量降低^{[24, 25]}, 进而导致干旱指数的降低。

表1 影响干旱指数变化的气候因子的变化趋势和相关系数 Table 1 Trends in and correlation coefficient among climate factors that influence AI in Qinghai

2.4 干旱指数与AO和ENSO的相互关系

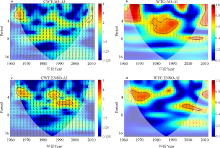
交叉小波变换(XWT)和小波相干变换(WTC)用于分析干旱指数与其它气候要素之间的多时间尺度的相关关系, 前者突出干旱指数变化与大尺度气候要素在时频域中高能区的相互关系, 后者则突出干旱指数变化与气候要素在时频域中低能区的相互关系。图4所示的箭头方向反映了两者相位关系^[19], 其中从左向右表示同相位, 从右向左表示反相位, 垂直向下的箭头则表示气候指数变换比干旱指数落后90° , 垂直向上的箭头表示气候指数变换比干旱指数提前90° 。

Figure Option
View Download New Window

图4 干旱指数(AI)与AO和MEI的交叉小波功率谱、相干小波功率谱
注:图a、c为交叉小波功率谱, b、d为相干小波功率谱; 粗黑线范围显示红噪声标准谱通过了α =0.05显著性水平下的检验, 细黑线包络显示了COI(cone of influence, 小波影响锥, 表示连续小波变换的数据边缘效应影响较大的区域)区域, 在该曲线以外的功率谱由于受到边界效应的影响而不予考虑。Fig.4 The Cross wavelet transform and wavelet coherence of the AI with AO and MEI
Note: Figure a and c is cross wavelet power spectrum, b and d is the correlation of the wavelet power spectrum. Bold black line show red noise standard spectral by the level of significance α =0.05 test. Fine black line show the envelope of COI area (cone of influence, the influence of wavelet cone, the data of continuous wavelet transform edge effect influence the larger area), outside the curve of the power spectrum not consider due to the influence of boundary effect.

青海省干旱指数与AO指数在1962-1970年间存在1~3年共振周期, 在此频率上有共振关系, 平均位相角接近水平向左90° , 则干旱指数变化位相与AO相反(图4a); 1962-1974年间和1978-1996年间, 小波相干功率谱在低能量区分别存在0~4和4~6年的共振周期(小波相干谱相关性通过了显著性水平α =0.05下的红噪音标准谱检验)(图4b)。青海省干旱指数与ENSO指数在1965-1974年间存在2~4年的共振周期(图4c), 在1982-2000年间表现出3~6年的共振周期; 1964-1976年间小波相干功率谱在低能区存在4~6年的主振荡周期(图4d), 在1996-2008年间存在5~6年的振荡周期, 但其频段的相关性较弱, 未通过α =0.05的红色噪音标准谱检验。

3 讨论与结论

由于干旱是一种非常复杂的气象现象, 其影响程度又是土壤水分亏缺及其持续时间的函数, 而干旱指数是反映气候干旱程度最常用的一个评价指标, 其结合影响干旱的气候、水文等参数, 可以对干旱的持续时间、发生频率和强度以及程度等进行分析^[26]。本研究选取AI指标对青海省地表干湿状况进行分析, 发现研究区干旱指数的变化趋势均呈现出下降趋势, 且下降趋势的空间分布相对复杂。再者, 由于干旱指数受多气象因子(例如:降水、气温等)影响, 所以研究区干旱指数的变化趋势表现出空间的差异性^[27]。已有研究表明, 青海省在1961-2010年间气温呈现上升趋势、降水量呈现增加的趋势, 但降水增加的幅度远大于温度上升的幅度; 而风速和日照时数却呈显著下降趋势^{[21, 28]}。这表明该地区近53年来气候有向暖湿变化的趋势, 这也进一步表明该地区干旱指数有降低的趋势。此外, 青海省降水主要集中在夏、秋两季, 夏、秋季降水分别约占全年降水量的60%和22%, 冬季降水仅占全年的3%^[21]; 该区域多年来四季日照时数和风速均呈下降趋势, 这可能是导致青海省各月份之间干旱指数变化差异显著的主要原因。

通过上述分析得出以下结论:1)近53年来, 青海省多年平均干旱指数为0.49, 整体呈现出波动降低趋势, 其线性降低速率为-0.03· 10 a^-1 (α =0.01), 表明青海省气候有变湿的趋势。青海省干旱指数有明显的季节变化特征, 表现为先减小后增加趋势, 呈波谷状分布, 12月出现最大值, 8月出现最小值。最高值出现在西北部的茫崖和中北部的格尔木和诺木洪, 最低值出现在中南部的曲麻菜和久治。2) 青海省干旱指数主要与日照时数和风速总体呈现显著的正相关关系, 其相关系数分别为0.436和0.324; 而与温度和降水呈显著负相关关系(P< 0.05)。3) 交叉小波变换与小波相干分析表明:青海省干旱指数与北极涛动(AO)和厄尔尼诺-南方涛动(ENSO)指数等存在多尺度的显著相关性(α =0.05)。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	沈永平, 王国亚. IPCC第一工作组第五次评估报告对全球气候变化认知的最新科学要点[J]. 冰川冻土, 2013, 35(5): 1068-1076. [本文引用:1]
[2]	张守红, 刘苏峡, 莫兴国, 舒畅, 孙杨, 张春. 阿克苏流域气候变化对潜在蒸散量影响分析[J]. 地理学报, 2010, 65(11): 1363-1370. [本文引用:1]
[3]	马柱国, 符淙斌. 中国北方干旱区地表湿润状况的趋势分析[J]. 气象学报, 2001, 59(6): 737-746. [本文引用:3]
[4]	沈彦军, 李红军, 雷玉平. 干旱指数应用研究综述[J]. 南水北调与水利科技, 2013, 11(4): 128-133. [本文引用:2]
[5]	王黎俊, 刘彩红, 孙安平, 伏洋, 朱西德. 近45年青海省夏季降水异常特征分析[J]. 干旱地区农业研究, 2008, 26(2): 225-230. [本文引用:1]
[6]	杨东, 王慧, 程军奇, 郭佩佩. 近50年青海省气候变化特征及其与ENSO的关系[J]. 生态环境学报, 2013, 22(4): 547-553. [本文引用:2]
[7]	Thornthwaite C W. An approach toward a rational classification of climate[J]. Geogrophical Review, 1948, 38(1): 55-94. [本文引用:2]
[8]	吴绍洪, 尹云鹤, 郑度, 杨勤业. 青藏高原近30年气候变化趋势[J]. 地理学报, 2005, 60(1): 3-11. [本文引用:2]
[9]	郝振纯, 江微娟, 鞠琴, 李丽, 王加虎, 鲁承阳, 畅俊杰. 青藏高原河源区气候变化特征分析[J]. 冰川冻土, 2010, 32(6): 1130-1135. [本文引用:1]
[10]	汪青春, 秦宁生, 唐红玉, 陈芳, 祁如英. 青海高原近44年来气候变化的事实及其特征[J]. 干旱区研究, 2007, 24(2): 234-239. [本文引用:1]
[11]	王颖华. 青海省降水与气温的时空变化规律研究[D]. 杨凌: 西北农林科技大学硕士学位论文, 2013. [本文引用:1]
[12]	汪宝龙, 张明军, 魏军林, 王圣杰, 马潜. 1960-2009年青海省极端降水事件的变化特征[J]. 水土保持通报, 2012, 32(4): 92-96. [本文引用:1]
[13]	张晓, 李净, 姚晓军, 孙美平. 近45年青海省降水时空变化特征及突变分析[J]. 干旱区资源与环境, 2012, 26(5): 6-12. [本文引用:1]
[14]	马全, 张鑫, 廖清飞, 徐静, 姚瑶. 青海省1961-2006年气温时空变化特征研究[J]. 西北农林科技大学学报(自然科学版), 2012, (40)11: 59-65. [本文引用:1]
[15]	白爱娟, 假拉, 徐维新. 基于潜在蒸散量对青海湖流域干旱气候以及影响因素的分析[J]. 干旱区地理, 2011, 34(6): 949-957. [本文引用:1]
[16]	Wolter K, Timlin M S. Monitoring ENSO in COADS with a seasonally adjusted principal component index[A]. Proceedings of the 17th Climate Diagnostics Workshop[C]. Oklahoma: Norman, OK, NOAA/NMC/CAC, NSSL, Oklahoma Climate, Survey CIMMS and the School of Meteorology, University of Oklahoma, 1993: 52-57. [本文引用:1]
[17]	Allen R G, Perreira L S, Raes D. Crop evapotranspiration——Guidelines for computing crop water requirements[R]. FAO irrigation and drainage paper 56. Rome, 1998. [本文引用:1]
[18]	Grinsted A, Moore J C, Jevrejeva S. Application of the cross wavelet transform and wavelet coherence to geophysical time series[J]. Nonlinear Processes in Geophysics, 2004, 11(5-6): 561-566. [本文引用:1]
[19]	Torrence C, Compo G P. A practical guide to wavelet analysis[J]. Bulletin of the American Meteorological Society, 1998, 79(1): 61-78. [本文引用:2]
[20]	张克新, 潘少明, 曹立国, 王允, 吴孟孟, 赵一飞. 横断山区季风期水分盈亏量时空变化特征及其与若干气候指数的相关性分析[J]. 自然资源学报, 2014, 29(11): 1869-1877. [本文引用:1]
[21]	郭素荣. 1960-2010年青海省气候变化的时空特征分析[D]. 兰州: 西北师范大学硕士学位论文, 2012. [本文引用:3]
[22]	Huo Z L, Dai X Q, Feng S Y, Kang S Z, Huang G H. Effect of climate change on reference evapotranspiration and aridity index in arid region of China[J]. Journal of Hydrology, 2013, 492: 24-34. [本文引用:1]
[23]	Zhang K X, Pan S M, Zhang W, Xu Y H, Cao L G, Hao Y P, Wang Y. Influence of climate change on reference evapotranspiration and aridity index and their temporal-spatial variations in the Yellow River Basin, China from 1961 to 2012[J]. Quaternary International, 2015, 380-381: 75-82. [本文引用:1]
[24]	王文玉, 杨沈斌, 张强, 吕开龙, 孙翔宇, 肖雯, 胡勇. 近50年环青海湖高寒地区和环鄱阳湖湿润地区潜在蒸散变化比较分析[J]. 中国沙漠, 2013, 33(3): 866-873. [本文引用:1]
[25]	马雪宁, 张明军, 王圣杰, 马潜, 潘淑坤. “蒸发悖论”在黄河流域的探讨[J]. 地理学报, 2012, 67(5): 645-656. [本文引用:1]
[26]	张彦龙, 刘普幸, 王允. 基于干旱指数的宁夏干旱时空变化特征及其Morlet小波分析[J]. 生态学杂志, 2015, 34(8): 2373-2380. [本文引用:1]
[27]	王英舜, 贺俊杰. 1961-2010年锡林浩特地区夏季降水量特征的小波分析[J]. 草业科学, 2014, 31(11): 2021-2025. [本文引用:1]
[28]	李晓东, 胡爱军, 祁栋林, 李凤霞, 王力, 刘吉宏. 近53年青海省气候变化与粮食产量及气候生产潜力特征[J]. 草业科学, 2015, 32(7): 1061-1068. [本文引用:1]

2013

0.0

沈永平, 王国亚. IPCC第一工作组第五次评估报告对全球气候变化认知的最新科学要点[J]. 冰川冻土, 2013, 35(5): 1068-1076.

2013年9月27日, 在瑞典首都斯德哥尔摩, 联合国政府间气候变化专门委员会第一工作组第五次评估报告《Climate Change 2013: The Physical Science Basis》决策者摘要(Summary for Policymakers, SPM)发布, 随后于9月30日公布了报告全文. 报告指出, 全球气候系统变暖的事实是毋庸置疑的, 自1950年以来, 气候系统观测到的许多变化是过去几十年甚至近千年以来史无前例的. 全球几乎所有地区都经历了升温过程, 变暖体现在地球表面气温和海洋温度的上升、海平面的上升、格陵兰和南极冰盖消融和冰川退缩、极端气候事件频率的增加等方面. 全球地表持续升温, 1880-2012年全球平均温度已升高0.85 ℃[0.65～1.06 ℃]; 过去30 a, 每10 a地表温度的增暖幅度高于1850年以来的任何时期. 在北半球, 1983—2012年可能是最近1 400 a来气温最高的30 a. 特别是1971-2010年间海洋变暖所吸收热量占地球气候系统热能储量的90%以上, 海洋上层(0～700 m)已经变暖. 与此同时, 1979-2012年北极海冰面积每10 a以3.5%～4.1%的速度减少; 自20世纪80年代初以来, 大多数地区多年冻土层的温度已升高. 全球气候变化是由自然影响因素和人为影响因素共同作用形成的, 但对于1950年以来观测到的变化, 人为因素极有可能是显著和主要的影响因素. 目前, 大气中温室气体浓度持续显著上升, CO 2 、 CH 4 和N 2 O等温室气体的浓度已上升到过去800 ka来的最高水平, 人类使用化石燃料和土地利用变化是温室气体浓度上升的主要原因. 在人为影响因素中, 向大气排放CO 2 的长期积累是主要因素, 但非CO 2 温室气体的贡献也十分显著. 控制全球升温的目标与控制温室气体排放的目标有关, 但由此推断的长期排放目标和排放空间数值在科学上存在着很大的不确定性.

... 在北半球,1983-2012年可能是最近1 400 年来气温最高的30年^[1] ...

2010

0.0

张守红, 刘苏峡, 莫兴国, 舒畅, 孙杨, 张春. 阿克苏流域气候变化对潜在蒸散量影响分析[J]. 地理学报, 2010, 65(11): 1363-1370.

Evapotranspiration is one of the key components of hydrological processes. Assessing the impact of climate factors on reference evapotranspiration (RET) is helpful in understanding the impact of climate change on hydrological processes. In this paper, based on the daily meteorological data from 1960 to 2007 within and around Aksu River basin, RET was estimated with the FAO Penman-Monteith Method. The temporal and spatial variations of PET were analyzed by using ARCGIS. Multiple Regression Analysis was employed to differentiate the effects of the variations of air temperature, solar radiation, relative humidity, vapor pressure and wind speed on PET. The results showed that RET in the eastern plain area of Aksu River Basin was about 1100 mm, which was nearly twice as much as that in the western mountain area.

1. Key Laboratory of Water Cycle & Related Land Surface Processes, Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China; 2. Graduate University of Chinese Academy of Sciences, Beijing 100049, China

蒸散发是水文过程的关键环节，研究气候因子对潜在蒸散发的影响，有助于深入认识水文过程对气候变化的响应。本文基于阿克苏河流域1960-2007 年逐日气象资料和Penman-Monteith公式，估算并分析参考作物蒸散量(RET) 时空变化特征，并用多元回归方法定量区分气候因子变化对RET 变化的贡献率。研究发现流域RET 空间差异明显，东部平原区平均年RET 为1100mm左右，是西部山区的近2 倍；东南部绿洲区的RET显著减少，而西部变化复杂。RET变化趋势的季节差异也很显著，以夏季变幅最大，是年变化的主要贡献者。高海拔地区相对湿度对RET变化影响最大，其它区域的风速变化对RET变化的贡献率最高。库车和乌恰站的风速变化对RET变化的贡献率大于50%，是RET变化的主导因素。

... 持续的全球变暖将影响全球和区域水循环的各个环节,除通过降水和气温变化影响流域径流外,还通过不同的方式对蒸散量产生了重要影响^[2] ...

2001

0.0

马柱国, 符淙斌. 中国北方干旱区地表湿润状况的趋势分析[J]. 气象学报, 2001, 59(6): 737-746.

Based on the 160 observ ational station's dat a of monthly precipitation and mean monthly temperature over China from 1951 to 1997,by use of the surface humid index computed from the data, H i= P / P e ( P is the monthly total of precipitation, P e the potential evaporation from air temperature),the interannual variation,decadal variation and the seaso nal differences of the sur face humid index,precipitation and temperature over two ty pical drought regions,the northwestern and northern China,have been analyzed.The geogr aphical distributions and trends of surface humid index have been given in the areas.The results indicated that the interannual and decadal variation of surface humid index over northren China is contrary to that of the west region of north western China,the form ershowed the wetting trend,and the latter drying trend.Also,the results show ed that the drying trend of northern China generally occurred in summer and autumn,and that the wetting trend occurred in various seasons in northw estern China except for autumn of the east region of nor thwestern China,and summer of westregion of northwestern China.

利用1951～1997年中国160站月降水和平均气温资料,通过计算的地表湿润指数 H i= P / P e ( P 为观测的月降水总量,Pe为月最大潜在蒸发),对比分析了中国华北、西北两个典型干旱区区域平均地表湿润指数的年代年际变化特征及季节性差异,并讨论了它与降水和气温的联系。最后,给出了地表湿润指数年及各季节变化趋势的地理分布。研究表明:西北西部和华北地区的年际及年代际变化趋势基本相反,前者地表为变湿趋势,后者为变干趋势。华北地区的干化趋势主要发生在夏秋季节,而西北除东部的秋季和西部的夏季外,其它季节均存在变湿趋势。

... 中国是世界上主要的干旱国家之一,干旱半干旱区面积占全国土地面积的50%以上,且主要集中在中国北方地区^[3,4] ...

... 干旱事件及其影响程度大小的分析和评价需要一定的量化标准^[3],但由于干旱是一种非常复杂的气象现象,对其出现和持续时间与下垫面的状况密切相关,至今对干旱的定义与强度没有一个统一的标准^[3,4,5] ...

2013

0.0

... 中国是世界上主要的干旱国家之一,干旱半干旱区面积占全国土地面积的50%以上,且主要集中在中国北方地区^[3,4] ...

2008

0.0

2013

0.0

... 干旱指数(Aridity Index,AI)是判断气候变化的重要指标,它以同期潜在蒸散量和降水量的差再与潜在蒸散量的比值来表示^[6,7],并以此来表示地表的干湿状况 ...

... 5 ℃),是典型的大陆性高原气候,为我国气候变化较为敏感的区域之一^[6,8] ...

1948

0.0

... s^-1,太阳辐射强,年日照时数超过2 500 h,是中国总辐射最大的省份之一^[7] ...

2005

0.0

吴绍洪, 尹云鹤, 郑度, 杨勤业. 青藏高原近30年气候变化趋势[J]. 地理学报, 2005, 60(1): 3-11.

The Tibetan Plateau is one of the best places to study global climate change. Aridity or humidity status of land surface is an important outcome that has close relations with a set of climatic factors such as precipitation, temperature, solar radiation, relative humidity and wind, but the relationship between them is complicated. This paper calculated potential evapotranspiration by applying Penman-Monteith model which was recommended by FAO in 1998, and aridity index by Vyshotskii model to indicate aridity or humidity status of the Tibetan Plateau during the period 1971-2000. Then it analyzed the changing trends of observed climatic factors (temperature and precipitation) and calculated factors (potential evapotranspiration and aridity index), and showed the spatial distribution of aridity/humidity status over the Tibetan Plateau during the period 1971-2000. Trends calculated by linear regression were tested through Mann-Kendall test. Results of 77 meteorological stations on the Tibetan Plateau showed that the main trends of climate change are temperature rise and precipitation increase; potential evapotranspiration decrease and most of the areas was ascending to more humid status. Results suggested that aridity or humidity status cannot be presented only with precipitation.

1. Institute of Geographic Sciences and Natural Resources Research, CAS, Beijing 100101, China; 2. Institute of Tibetan Plateau Research, CAS, Beijing 100085, China; 3. Graduate School of the Chnese Academy of Sciences, Beijing 100039, China

以1971~2000年青藏高原77个气象台站的观测数据 (最低、最高气温,日照时数,相对湿度,风速和降水量) 为基础,应用1998年FAO推荐的Penman-Monteith模型,并根据我国实际状况对其辐射项进行修正,模拟了青藏高原1971~2000年的最大可能蒸散,并由Vyshotskii模型转换为干燥度,力求说明近30年青藏高原的气候变化趋势,以及干湿状况的空间分布。应用线性回归法计算变化趋势,并用Mann-Kendall方法进行趋势检验。结果表明：青藏高原近30年气候变化的总体特征是气温呈上升趋势,降水呈增加趋势,最大可能蒸散呈降低趋势,大多数地区的干湿状况有由干向湿发展的趋势。气候因子与地表干湿状况间并不是线性关系,存在很大的不确定性。

... 5 ℃),是典型的大陆性高原气候,为我国气候变化较为敏感的区域之一^[6,8] ...

... 利用同期潜在蒸散量和降水量的差值,再与潜在蒸散量的比值来表示干旱指数^[8],计算公式如下: ...

2010

0.0

郝振纯, 江微娟, 鞠琴, 李丽, 王加虎, 鲁承阳, 畅俊杰. 青藏高原河源区气候变化特征分析[J]. 冰川冻土, 2010, 32(6): 1130-1135.

利用1954-2007年青藏高原河源区（包括长江、黄河、澜沧江、怒江和雅鲁藏布江）30个气象站的年平均气温和降水量，通过计算气候倾向率和距平小波分析（墨西哥帽小波函数）等方法分析了近54a来青藏高原河源区的气候变化特征. 结果表明：青藏高原河源区年平均气温变化在7～-3℃之间，由东南向西北逐渐减少；并呈现逐年上升的趋势，自20世纪90年代以来升温更为强烈. 年降水量的分布大致是由东南向西北逐步减少，在同一纬度上，东部的降水量多于西部，2001-2005年的多年平均降水量达到历史最大值. 年平均气温和降水的周期振荡在高频区振荡频繁，有多个突变点，中低频区则较平缓. 不同河源区的气温增温率具有显著的区域性差异，雅鲁藏布江源区最大（0.54℃ ．（10a） -1 ），黄河次之（0.31℃ ．（10a） -1 ），澜沧江和怒江最小（0.17℃ ．（10a） -1 ）. 除少数气象站外，区域内各站的年平均气温也普遍升高. 澜沧江源区是整个青藏高原河源区降水量升幅最大的地区，而雅鲁藏布江源区为降水量升幅最小的区域. 从整个青藏高原来看，温度和降水均普遍升高，整个区域呈现暖湿化趋势，但降水量的增加较微弱.