引用本文
王杰, 李卫朋. 基于灵活的时空融合模型的植被覆盖度与植被指数关系. 草业科学, 2017,34(2):264-272
Wang Jie, Li Wei-peng. Research on relationship between vegetation cover fraction and vegetation index based on flexible spatiotemporal data fusion model. Pratacultural Science,2017,34(2): 264-272  
Permissions
Copyright©2017, 《草业科学》编辑部
《草业科学》编辑部
基于灵活的时空融合模型的植被覆盖度与植被指数关系
王杰, 李卫朋
西华师范大学国土资源学院,四川 南充 637009
通信作者:王杰(1984-),男,四川南充人,讲师,博士,主要从事遥感数字图像处理、数据挖掘研究工作。E-mail:[email protected]
收稿日期: 2016-07-01
基金: 西华师范大学博士科研启动基金(412546、412547); 四川省教育厅自然科学重点项目(17AZ0387); 国家自然科学基金资助项目(41101348)
摘要

时空数据融合模型被广泛地应用于获取高时间、高空间分辨率的植被指数与植被覆盖度,但是其反演的精度常常受输入的低空间分辨率影像(如MODIS影像)的影响。本研究基于灵活的时空数据融合方法(FSDAF),深入分析了赛里木湖流域与石河子地区两种不同情景的MODIS影像组合对FSDAF模型植被覆盖度提取精度的影响,并研究了6种植被指数与植被覆盖度的线性与非线性关系。研究结果表明,FSDAF模拟影像的植被覆盖度精度取决于2个时期MODIS影像的变化率,影像变化小时取得的精度明显好于影像差异大的情况。而采用植被指数对植被覆盖度模拟时,NDVI与OSAVI的线性拟合效果较好,可以获取较理想的结果。试验表明,采用时空模型用于研究区植被覆盖反演能取得较好的效果,具有一定的应用推广价值。

关键词: 时空融合模型; 灵活的时空融合模型; 植被覆盖度; 植被指数; Landsat TM; MODIS; 线性与非线性拟合
中图分类号:S127 文献标志码:A 文章编号:1001-0629(2017)2-0264-09 doi: 10.11829/j.issn.1001-0629.2016-0256
Research on relationship between vegetation cover fraction and vegetation index based on flexible spatiotemporal data fusion model
Wang Jie, Li Wei-peng
College of Land and Resources, China West Normal University, Nanchong 637009, China
Corresponding author: Wang Jie E-mail:[email protected]
Abstract

The spatiotemporal data fusion model has been widely used to obtain high temporal and spatial resolution vegetation indexes and vegetation cover fractions, but its accuracy is often affected by low spatial resolution images [e.g., moderate resolution imaging spectroradiometer (MODIS) images]. This study design was based on the flexible spatiotemporal data fusion model (FSDAF), and investigated the effects of three different MODIS image pairs of the FSDAF model for vegetation cover fraction extraction in arid region of China. Furthermore, the linear and non-linear relationships between six vegetation indexes and vegetation cover fractions were investigated. The results showed that the retrieval accuracy of the vegetation cover fraction of FSDAF simulated images depended on the rate of change of the MODIS images in two periods. In addition, the accuracy of the image with a slight change was significantly higher than that of the image with a great difference. When vegetation indexes were used to simulate the vegetation cover fraction, the normalized difference vegetation index (NDVI) and green NDVI (GNDVI) linear fitting methods produced better results than other methods did, and provided the ideal results. The experimental results showed that the FSDAF model could be used to determine the retrieval of vegetation cover in arid area, and it had a good effect and applicability.

Keyword: Spatiotemporal Data Fusion Model; Flexible Spatiotemporal Data Fusion Model; Vegetation Cover Fraction; Vegetation Index; Landsat TM; Moderate Resolution Imaging Spectroradiometer; Linear and Nonlinear Fitting

植被覆盖度通常是指植被冠层垂直投影面积占基准地表单位面积的百分比[1], 其获取方式有地面监测和遥感监测两种方法, 与耗时耗力的人工量测相比, 通过遥感手段反演植被盖度信息是一种有效快捷的方法[2]。陆地卫星TM/ETM提供了较高空间分辨率的数据, 其被广泛应用于土地覆盖与土地利用变化监测之中[3]。但是, 因其较低的时间分辨率很难应用于全球生物动态变化监测[4]。在常年多云地区, 每年仅有2~3幅影像可供使用[5, 6, 7]。Terra与Aqua平台的MODIS传感器提供了逐日的全球观测数据, 能够快速地获取地表植被的变化。然而, 其空间分辨率较低, 不能刻画异质性较大区域的变化过程。

为了解决时间和空间分辨率对植被覆盖度反演的影响, 国内外学者采用数据融合的方法提高反演精度, 比如HIS变换[8]、主成分替代[9]、小波分解[10]。Gao等[11]提出了一种空间与时间自适应辐射率融合模型(STARFM)。 STARFM模型引入光谱邻域相似的信息权重融合两类数据, 将MODIS影像同质性区域的反射率变化应用于TM/ETM影像。大量的模拟与预测试验表明, 如果MODIS影像上存在大量的同质性像元, STARFM模型能够有效地预测反射率影像, 但像元空间分辨率低、混合像元严重时难以取得较高的精度[12]。基于STARFM的增强型ESTARFM模型[5]采用混合像元分解算法, 针对同质性与异质性区域采用不同的转换系数, 模型精度有了较大的提升, 但在时相差异较大或者云量较多时模拟的精度比STARFM低[6]。为了准确地预测高精度的Landsat影像, 克服巨大异质性突变区域带来的预测误差, Zhu等[7]提出了灵活的空间时间数据融合算法(Flexible Spatiotemporal Data Fusion Model, FSDAF), FSDAF模型只需要参考时间点的TM/ETM和MODIS影像, 以及预测时间点的MODIS影像, 可有效地降低数据输入量。

由于云的覆盖, 大量的TM/ETM影像无法直接应用于植被覆盖率的估算, 在Landsat TM/ETM影像可选择性有限的情况下, 通过时间与空间分辨率融合算法可获取高空间、时间分辨率的植被覆盖度与植被指数影像。在时空融合模型中, 当选择数据质量较高的高空间分辨率影像后(如无云的Landsat TM影像), 时空融合模型下的植被覆盖度反演的精度常常受到输入模型的低空间分辨率影像(如MODIS影像)的影响。故而, 研究低空间分辨率的遥感影像变化对植被覆盖度与植被指数的定量算法具有重要意义。针对这一问题, 本研究基于FSDAF模型, 探讨不同变化强度的低空间分辨率遥感影像输入融合模型对植被覆盖度精度提取的影响, 并分析了6种植被指数与植被覆盖度的线性与非线性关系。

1 研究方法

本研究基于FSDAF模型分析植被覆盖度与植被指数的关系, 针对不同变化强度的MODIS影像进行融合, 主要研究其对植被覆盖度与植被指数精度反演的影响。首先, 利用FSDAF模型融合成预测时间点的TM影像, 然后利用预测点的真实TM影像对融合影像进行精度检验。在此基础上, 获取及评价融合的TM影像植被覆盖度, 研究植被覆盖度与植被指数的线性与非线性关系。

1.1 灵活的时空数据融合模型

在FSDAF模型中, 输入数据包括一对不同时间的低空间分辨率影像(分别为t1与t2时刻), 以及一幅高空间分辨率的影像(为t2时刻), 在实施数据融合方法之前, TM和MODIS影像应校准到同一个物理量, 如大气顶部反射率或表面反射率。FSDAF融合模型主要包括6个步骤:(1)t1时刻的高空间分辨率影像(Landsat)分类; (2)估计从t1时刻到t2时刻高时间分辨率影像(如 MODIS影像)每个类别的时间变化; (3)预测t2时刻的Landsat影像使用类别尺度的时间变化和计算MODIS影像每个像素预测的残差; (4)利用t2时刻的MODIS影像, 使用薄板样条函数预测高空间分辨率影像(如 Landsat TM影像); (5)基于薄板样条函数的残差分布计算; (6)利用邻域信息得到Landsat TM影像的最终预测。

在FSDAF模型中, 需要对输入的TM/ETM进行分类。根据分类的方法不同, 可以将FSDAF模型分为监督与非监督, 其中非监督的FSDAF模型采用ISODATA算法, 监督的FSDAF模型采用支持向量机算法。如果选择云量极少的t1时刻Landsat TM影像, 那么模型的精度主要受两景MODIS影像的影响, 两景MODIS影像在融合模型中的主要作用是在于获取两个时间点的地物变化, 故而, 不同变化强度的MODIS影像组合对FSDAF模型精度的影响需要进行深入的研究, 这就是本研究的出发点及数据选择标准。对于FSDAF模型的详细叙述, 可以参考文献[7], 这里不再赘述。

1.2 植被指数与植被覆盖度的关系

获取改正的植被覆盖度之后, 计算MODIS影像的各种植被指数, 包括差值植被指数(DVI)[13]、归一化绿波段差值植被指数(GNDVI)[14]、归一化植被指数(NDVI)[15]、优化土壤调节植被指数(OSAVI)[16]和比值植被指数(RVI)[17]。同时, 去除MODIS影像的第6波段, 用TM影像的缨帽变换[18]系数矩阵与MODIS影像进行变换, 获取三波段的变换结果, 这里只有绿度波段被保留下来, 其余波段删除。各种植被指数的计算公式如(1)-(5)所示。获取各种植被指数之后, 将TM影像获取的植被覆盖度与MODIS影像的植被指数进行线性与非线性拟合。目前, 植被覆盖度与植被指数的线性与非线性拟合较好[19, 20], 采用Mu等[21]的线性与非线性公式, 以此验证植被覆盖度与植被指数的线性与非线性关系, 其表达式如式(6)所示。其中, FVC是植被覆盖度, VI是各种植被指数, a、b、k是参数, 当k为1时, FVC与VI呈线性关系, 当k不为1时, 呈现非线性关系。均方根误差(RMSE)、标准差、相关系数(皮尔逊相关系数)作为评价指标, 综合评价各种植被指数与植被覆盖度的拟合精度。假定植被覆盖度与植被指数线性不相关(k不等于1), 然后对这个三变量的等式求解偏导数, 采用Levenberg-Marquardt算法进行拟合。

DVI=ρ NIP-ρ PEA(1)

GNDVI= ρNIR-ρGREENρNIR+ρGREEN(2)

NDVI= ρNIR-ρREDρNIR+ρRED(3)

OSAVI= ρNIR-ρREDρNIR+ρRED+0.16(4)

RVI= ρNIRρRED(5)

FVC=(aVI+b)k(6)

1.3 研究区及数据处理

本研究应选择覆盖大量植被且云量较小的典型区域, 因而本研究以满足此要求的赛里木湖流域与石河子地区为研究区。

根据MODIS影像地物变化的大小进行不同组合, 得到两个类型的数据输入情景, 它们分别是:t1与t2时间点的MODIS影像上地物变化极小, 且影像上条纹极少; t1与t2时间点的MODIS影像上地物有微小的变化, 影像上有部分条纹。针对这两个例子, 分别下载无云或者云量极少的同一天的TM和MODIS影像(包括t2时间点的TM影像, 用以验证不同例子的融合结果)。其中, 使用的TM影像编号及云量如表1所示, 在每个例子中, 第一景影像输入融合模型参与预测过程, 第二景影像为真实的TM影像(作为验证融合模型的影像)。

表1 TM影像列表及云量大小 Table 1 Thematic mapper (TM) image list and cloud content

对TM原始影像先进行辐射定标, 将数值转换为辐射值, 其中需要Gain与Bias系数, 这里从参考文献[22]获取。然后进行波段合并, 最后进行大气校正, 大气校正采用ENVI5.3的FLAASH模块。MODIS影像采用表面反射率产品MOD09GA, 此产品已经过严格的大气校正、几何校正和辐射校正, 空间分辨率为500 m, 包含7个波段(620-670, 841-876, 459-479, 545-565, 1 230-1 250, 1 628-1 652, 2 105-2 155 nm)。首先对MODIS影像进行预处理, 将HDF格式的影像转换成ENVI标准格式, 重新投影MOD09GA产品, 使其与TM影像坐标一致。波段合并且按照波长大小升序排列。最后用TM影像裁剪出其对应的MODIS影像, 处理成反射率的TM影像与裁剪出的MODIS影像分别见图1、2、3(影像都以7、4、1波段合成进行显示)。

图1 赛里木湖流域原始影像与FSDAF模型预测结果Fig. 1 Original image of Sailimu Lake watershed and simulated flexible spatiotemporal data fusion (FSDAF) model image

图2 石河子地区原始影像与FSDAF模型预测结果Fig. 2 Original image of Shihezi district and the simulated flexible spatiotemporal data fusion (FSDAF) model image

图3 石河子地区验证影像、非监督FSDAF模型、监督FSDAF模型分类提取的植被覆盖度Fig. 3 Extraction vegetation cover fraction of validation image, unsupervised and supervised flexible spatiotemporal data fusion (FSDAF) model in Shihezi districte

2 结果和分析

非监督的FSDAF融合模型主要包括如下的输入参数:半窗口大小、类似像元的数目、最小类别、最大类别、块大小、尺度因子等。这些参数的设置需要根据遥感影像的空间分辨率与获取的精度要求而定, 经过多次的模拟发现, 它们分别设置为12、15、5、10、20、15较为合适。监督的FSDAF融合模型需要提前对经过大气校正的影像进行分类, 故而没有最小类别与最大类别参数的设置。监督分类都采用支持向量机算法(SVM), 此算法内置于ENVI软件中, 核函数采用径向基函数, 核函数的δ 值为0.167 0, 惩罚参数为100, 金字塔水平设置为1, 金字塔重分类阈值设置为0.9。在赛里木湖流域中, 设置类别的数目为7类, 分别是湖泊、冰雪、云、大田作物、林地、岩石和土壤。在石河子影像中, 设置类别的数目为5类, 分别是水体、大田作物、沙漠、土壤和建筑物。赛里木湖流域的四景TM影像分类, 参照相关研究[23]选择感兴趣区域及验证样本(总体精度都超过87%, kappa系数超过0.85), 为了更为准确地进行时空融合, 利用目视解译的方法改正分类错误的像元。针对石河子地区, 由于地物类别较为单一, 按照相关论文的处理过程[24], 准确选择各种分类样本及评价样本, 最终获取各种地类的分类结果(总体精度都超过92%, kappa系数超过0.90), 通过目视解译, 改正分类错误的像元。各种原始影像及FSDAF融合的结果以图1、2展示出来。

2.1 赛里木湖流域草地与耕地模拟及试验结果

图1前4幅影像分别是输入的2006年第233天的赛里木湖区域MODIS、TM影像和2006年第249天的MODIS影像、TM影像(作为验证影像)。根据图1原始TM影像与融合影像对比, 容易判读出预测的影像消除了云的影响, 这是由于两景MODIS影像无云, 这说明FSDAF融合模型具有去云的作用; 同时, FSDAF融合模型获取的TM影像颜色与原始影 像颜色基本一致, 仅仅湖泊的颜色略有差异; 此外, 观察植被、土壤、岩石与湖泊融合前后的光谱特性发现, FSDAF融合模型对植被、土壤、岩石的光谱保持较好, 而水体的光谱变化较大, 但这对植被覆盖度的提取影响不大。而后, 采用SVM分类算法对原始TM和融合影像进行分类, 对分类后的影像进行目视改正, 最后提取大田作物与林地的植被像元。经过比较发现, 原始影像获取的植被像元与非监督FSDAF融合模型相差6%, 监督FSDAF融合模型相差7%, 这说明FSDAF融合模型能够准确地提取植被覆盖度。为了验证MODIS影像的植被指数与植被覆盖度的关系, 将验证影像与两种融合算法获取的植被影像(0和1的二值影像)聚合到MODIS影像空间分辨率, 将二值影像的植被像元聚合成植被覆盖度, 其取值范围为0-1。然后, 以验证影像聚合获取的植被覆盖度作为参考数据, 评价两种融合算法获取的植被覆盖度精度, 采用公式(6)进行线性拟合(假定k=1), 非监督与监督FSDAF融合模型的a、b系数分别为0.925 0、0.060 0和0.913 0、0.070 0, 说明获取的植被覆盖度精度非常高, a系数趋近于1, 而b系数趋近于0。

最后, 按照公式(1)-(5)计算MODIS影像的各种植被指数, 同时获取其缨帽变换的绿度波段, 采用公式(6)对两种融合的植被覆盖度与MODIS影像计算的植被指数进行线性与非线性统计分析。可以发现, 各种植被指数都不能成功拟合, 于是设定k=1进行线性拟合。由于篇幅限制, 未置放统计结果于文章中, 而是集中评价石河子地区的融合结果, 将各种统计及评价指标详细罗列出来。经过统计对比发现, NDVI、OSAVI与FSDAF融合模型获取的植被覆盖度拟合精度较高, 但是它们的相关系数都较低, NDVI与两种FSDAF融合模型获取的植被覆盖度的相关性分别为0.663 0、0.657 0, 而OSAVI获取的相关性系数分别为0.661 0、0.654 0。

2.2 石河子市农田耕地模拟及试验结果

按照上述的过程, 对石河子地区的遥感数据进行融合(图2)。两景MODIS影像的质量相对赛里木湖地区影像较差, 植被区域出现大量的条纹与斑点状的像元。虽然影像质量不高, 但是它们具有相似的分布与变化。非监督与监督的FSDAF模型融合结果也有类似于第194天的MODIS影像条纹分布。采用像元聚合的方法获取的验证影像、非监督FSDAF模型、监督FSDAF模型分类提取的植被覆盖度如图3所示, 显然, FSDAF模型获取的植被覆盖度在左下角部分明显低于验证影像获取的植被覆盖度。同样, 采用公式(1)-(5)获取植被指数如图4所示(包含缨帽变换的绿度波段)。这里没有删除背景像元, 在程序设计的过程中, 通过设定FSDAF模型的植被覆盖度大于0的像元参与拟合, 就能快速地删除背景像元。首先, 以验证影像获取的植被覆盖度作为真值验证FSDAF模型获取的植被覆盖度, 其中, 验证区域的植被像元占总像元的37.266 0%(这里没有进行聚合), 非监督与监督分别为30.906 0%、28.385 0%(表2)。对于线性拟合验证影像植被覆盖度(经过像元聚合)与FSDAF融合模型获取的植被覆盖度而言, 其拟合系数a和b、均方根误差、标准差、相关系数可以看出, 非监督的FSDAF模型获取的石河子影像植被覆盖度相比监督方法精度更高, 但是其系数a小于赛里木流域拟合的系数, b又大于其系数, 这说明在石河子地区FSDAF模型获取的植被覆盖度精度低于赛里木流域。比较图1与图2中4个时期的MODIS影像发现, 图1中的MODIS影像的质量明显高于图2, 同时, 图1中的两景MODIS影像的植被变化较小, 而图2的两景MODIS影像中部区域植被稀疏明显。分析FSDAF融合模型的植被覆盖度提取的精度之后, 继续采用公式(6)对植被覆盖度与植被指数进行线性、非线性拟合, 拟合方法仍然使用赛里木湖流域的方法, 经过大量试验发现, 非线性拟合不成功, 仍然采用线性拟合的方式。表3与表4分别为非监督、监督的FSDAF融合模型获取参数统计, 从中可以看出, NDVI与GNDVI两种植被指数拟合的精度较高, 这也跟赛里木流域的拟合结果相似, 不过皮尔逊相关系数略微的降低, 主要原因在于两景MODIS影像质量较差, 不能完全捕捉到植被的变化信息。

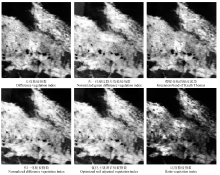图4 石河子地区MODIS影像提取植被指数Fig. 4 Extraction vegetation indexes DVI, GNDVI, Greenness, NDVI, OSAVI, and RVI in MODIS image of Shihezi district

表2 非监督与监督的FSDAF模型获取的植被覆盖度与真实覆盖度的线性关系 Table 2 Statistical results of retrieval vegetation cover fraction of FSDAF model and the true vegetation cover fraction
表3 非监督FSDAF模型获取的植被覆盖度与MODIS影像植被指数线性关系 Table 3 Statistical results of retrieval vegetation cover fraction of unsupervised FSDAF model and vegetation indexes of MODIS image
表4 监督FSDAF模型获取的植被覆盖度与MODIS影像植被指数线性关系 Table 4 Statistical results of retrieval vegetation cover fraction of supervised FSDAF model and vegetation indexes of MODIS image
3 讨论与结论

高动态的异质性区域的植被覆盖度定量反演需要高时空分辨率的遥感数据, 本研究利用FSDAF融合模型, 研究了植被覆盖度提取的精度, 以及植被覆盖度与植被指数的关系, 对两个研究区的结果进行分析与讨论后, 发现FSDAF融合模型对NDVI的预测能力较好, 能够获得可用性更高的NDVI时序数据, 这与前人[25]的结论一致。由于FSDAF融合模型预测的精度常常受所选MODIS影像的影响, 故而本研究讨论了两种MODIS影像对的情况, 验证了FSDAF融合模型对植被覆盖度与植被指数的反演精度。同时得到如下结论:

1)当两景MODIS影像对无云且地物时间变化极小时, FSDAF融合模型能够准确地预测出TM影像, 且精度最高。当两景MODIS影像对无云且随时间有少许变化时, 预测的TM影像质量有所降低。

2)植被覆盖度与植被指数的线性拟合的精度较高, 但是其相关性都较低。NDVI与OSAVI与植被覆盖度的线性拟合精度最高, 同时其相关性也是最高。在赛里木湖流域, NDVI与两种FSDAF融合模型获取的植被覆盖度的相关系数分别为0.663 0、0.657 0, 而OSAVI获取的相关性系数分别为0.661 0、0.654 0。在石河子地区, NDVI与两种FSDAF融合模型获取的植被覆盖度的相关性分别为0.537 2、0.531 4, 而OSAVI获取的相关性系数分别为0.537 2、0.531 4。

The authors have declared that no competing interests exist.

参考文献
[1] Purevdorj T, Tateishi R, Ishiyama T. Relationships between percent vegetation cover and vegetation indices. International Journal of Remote Sensing, 1998, 19(18): 3519-3535. [本文引用:1]
[2] 古丽·加帕尔, 陈曦, 马忠国. 干旱区稀疏芦苇盖度遥感信息提取. 干旱区地理, 2010, 33(6): 988-996.
Guli· Jiapaer, Chen X, Ma Z G. Extraction of vegetation fraction over the sparse reed in arid area. Arid Land Geography, 2010, 33(6): 988-996. (in Chinese) [本文引用:1]
[3] 蔡朝朝, 安沙舟, 蒲智, 淮永建. 基于TM NDVI的库尔勒市域植被覆盖动态变化. 草业科学, 2015, 32(7): 1069-1078.
Cai Z Z, An S Z, Pu Z, Huai Y J. A study on vegetation coverage change in Korla City based on the TM NDVI. Pratacultural Science, 2015, 32(7): 1069-1078. (in Chinese) [本文引用:1]
[4] 李亚刚, 李文龙, 刘尚儒, 秦兰兰. 基于遥感技术的甘南牧区草地植被状况多年动态. 草业科学, 2015, 32(5): 675-685.
Li Y G, Li W L, Liu S R, Qin L L. Grassland vegetation dynamics over the years based on remote sensing technology in Gannan pastoral area. Pratacultural Science, 2015, 32(5): 675-685. (in Chinese) [本文引用:1]
[5] Zhu X, Chen J, Gao F, Chen X, Masek J G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sensing of Environment, 2010, 114(11): 2610-2623. [本文引用:2]
[6] Emelyanova I V, McVicar T R, Van Niel T G, Li L T, van Dijk A I J M. Assessing the accuracy of blending Land sat-MODIS surface reflectances in two land scapes with contrasting spatial and temporal dynamics: A framework for algorithm selection. Remote Sensing of Environment, 2013, 133: 193-209. [本文引用:2]
[7] Zhu X, Helmer E, Liu D, Chen J, Gao F, Lefsky M. A flexible spatiotemporal method for fusing satellite images with different resolutions. Remote Sensing of Environment, 2016, 172: 165-177. [本文引用:2]
[8] Carper W J, Lilles T M, Kiefer R W. The use of intensity-huesaturation transformations for merging SPOT panchromatic and multispectral image data. Photogrammetric Engineering and Remote Sensing, 1990, 56: 459-467. [本文引用:1]
[9] Shettigara V K. A generalized component substitution technique for spatial enhancement of multispectral images using a higher resolution data set. Photogrammetric Engineering and Remote Sensing, 1992, 58: 561-567. [本文引用:1]
[10] Yocky D A. Multiresolution wavelet decomposition image merger of Land sat Thematic Mapper and SPOT panchromatic data. Photogrammetric Engineering and Remote Sensing, 1996, 62: 1067-1074. [本文引用:1]
[11] Gao F, Masek J, Schwaller M, Hall F. On the blending of the Land sat and MODIS surface reflectance: Predicting daily Land sat surface reflectance. IEEE Transactions on Geoscience and Remote Sensing, 2006, 44: 2207-2218. [本文引用:1]
[12] Hilker T, Wulder M A, Coops N C, Linke J, McDermid G, Masek J G, Gao F, White J C. A new data fusion model for high spatial and temporal resolution mapping of forest based on Land sat and MODIS. Remote Sensing of Environment, 2009, 113: 1613-1627. [本文引用:1]
[13] Tucker C J. A spectral method for determining the percentage of green herbage material in clipped sample. Remote Sensing of Environment, 1980, 9: 175-181. [本文引用:1]
[14] Gitelson A A, Kaufman Y J, Merzlyak M N. Use of a green channel in remote sensing of global vegetation from EOS-MODIS. Remote Sensing of Environment, 1996, 58: 289-298. [本文引用:1]
[15] Rouse J W, Haas R H, Schell J A, Deering D W. Monitoring vegetation systems in the Great Plains with ERTS. Proceedings of the Third ERTS Symposium. NASA, 1973, 1: 309-317. [本文引用:1]
[16] Rondeaux G, Steven M, Baret F. Optimization of soil adjusted vegetation indices. Remote Sensing of Environment, 1996, 55: 95-107. [本文引用:1]
[17] Jordan C F. Derivation of leaf area index from quality of light on the forest floor. Ecology, 1969, 50: 663-666. [本文引用:1]
[18] 梁顺林. 定量遥感. 北京: 科学出版社, 2009: 189-190.
Liang S L. Quantitative remote sensing of land surfaces. Beijing: Science Press, 2009: 189-190. (in Chinese) [本文引用:1]
[19] Xiao J, Moody A. A comparison of methods for estimating fractional green vegetation cover within a desert-to-upland transition zone in central New Mexico, USA. Remote Sensing of Environment, 2005, 98(2): 237-250. [本文引用:1]
[20] Li F, Kustas W P, Prueger J H, Neale C M, Jackson T J. Utility of remote sensing based two source energy balance model under low and high vegetation cover conditions. Journal of Hydrometeorology, 2005, 6(6): 878-891. [本文引用:1]
[21] Mu X H, Huang S, Ren H Z, Yan G J, Song W J, Ruan G Y. Validating GEOV1 fractional vegetation cover derived from coarse resolution remote sensing images over cropland s. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2015, 8(2): 439-446. [本文引用:1]
[22] Chand er G, Markham B L, Helder D L. Summary of current radiometric calibration coefficients for Land sat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sensing of Environment, 2009, 113: 893-903. [本文引用:1]
[23] 汪洋. 博斯腾湖流域土地利用变化与经济重心的迁移分析. 乌鲁木齐: 新疆大学博士学位论文, 2015: 18-43.
Wang Y. Land use conversion and migration of economy gravity center in the Bosten lake basin. PhD Thesis. Urumqi: Xinjiang University, 2015: 18-43. (in Chinese) [本文引用:1]
[24] 许西盼. 基于遥感影像的土地利用动态变化监测与预测模型研究(以石河子垦区为例). 石河子: 石河子大学硕士学位论文, 2010: 20-44.
Xu X P. Study on monitoring and prediction of land use change in Shihezi reclamation area by remote sensing. Master Thesis. Shihezi: Shihezi University, 2010: 20-44. (in Chinese) [本文引用:1]
[25] 赵艳丽. 时空融合技术在高时空分辨率NDVI数据重构中的应用. 太原: 太原理工大学硕士学位论文, 2015: 35-47.
Zhao Y L. Reconstruction of NDVI data with high-spatial and temporal resolution using spatial-temporal fusion technique. Master Thesis. Taiyuan: Taiyuan University of Technology, 2015: 35-47. (in Chinese) [本文引用:1]