第一作者:张仁平(1979-),男,甘肃甘谷人,副研究员,博士,主要从事草地遥感与地理信息系统研究。E-mail:[email protected]
利用新疆及周边地区的154个气象站点资料,采用反距离权重法(IDW)、普通克里金法(Kriging)、协同克里格法(Cokriging)、贝叶斯法(EBK)和ANUSPLIN软件5种方法,对新疆地区1995-2004年10年间的月降水量空间插值模拟结果进行了交叉检验。结果表明,在新疆地区,5种方法的插值精度表现为ANUSPLIN>Cokriging>EBK>Kriging>IDW,并随月份有所变化,平均绝对误差(MAE)和均方根误差(RMSE)表现为秋冬两季误差低于春夏两季,平均相对误差(MRE)的值在春季和秋季较高。与已建立的新疆的降水量分布格局进行比较发现,ANUSPLIN兼顾了插值曲面的准确度与平滑度,它较为准确地反映了新疆地区降水空间分布的特征,EBK法在4月和7月插值结果与实际偏差较大,而1月和10月插值效果较好,Cokriging法插值结果均质性较差,并不能反映新疆实际降水的空间分布。Kriging法在10月插值效果较好外,在其他3个月的插值效果不好,IDW法的最大值或者最小值主要分布在台站周围,与实际情况相差较远。
Based on the data from 154 meteorological stations in Xinjiang district and surrounding areas, five interpolation methods [inverse distance weighting (IDW), ordinary Kriging (Kriging), Collaborative Kriging (Cokriging), Empirical Bayesian (EBK) and ANUSPLIN spatial interpolation] were implemented for simulation and cross examination of monthly average precipitation from 1995 to 2004. The test results showed that the interpolation accuracy, from most to least accurate, was ANUSPLIN, Cokriging, EBK, Kriging and IDW. Accuracy varied between months. The Root Mean Square Error (RMSE) and the Mean Absolute Error (MAE) showed lower value in winter and spring than in summer and autumn; the Mean Relative Error (MRE) was higher in spring and autumn. While comparing precipitation distribution in Xinjiang, ANUSPLIN considered both the accuracy and smoothness of the interpolation surface, which more precisely reflected the spatial distribution of precipitation. Interpolation results from the EBK method were much higher than the actual precipitation distribution in April and July, while the interpolation was better in January and October. Cokriging interpolation results were uneven and did not accurately reflect spatial distribution. Interpolation using the Kriging method was better in October, but less so for the other three months (January, April and July). The maximum or minimum value of the IDW method was mainly distributed around the station and differed with the actual precipitation distribution.
降水量是反映一个区域环境变量的重要指标之一, 是最直接、最敏感的气候因素, 也是影响覆盖变化和植被格局的关键因素[1, 2]。降水量的空间化对于水资源状况分析、利用以及生态环境治理具有重要意义, 空间化降水量数据成为很多预测模型不可缺少的基础数据[3], 降水也是草原综合顺序分类法的重要指标之一[4]。由于新疆地区气象站分布稀疏, 全疆仅有国家级气象台站66个, 且多数气象台站分布在绿洲内, 而在海拔较高的区域基本上没有气象台站。新疆地区经纬度跨度大, 地形地貌复杂多变、降水量在新疆分布有明显的时空变化特征[5, 6]。仅依靠气象站点并不能满足科研和生产部门的要求, 如何利用有限的气象站点数据模拟新疆地区的空间降水量分布是很有必要的。
根据气象站点数据对未知点进行插值预测是降水量空间化的最有效途径[7, 8]。然而, 如何根据区域的特征与台站数据选择一种最适合当地的插值方法是一个难题[9, 10]。常用于气象要素的空间插值方法有反距离权重法、普通克里金法和协同克里格法等[1, 11]。然而, 不同的研究时间尺度和区域需选用不同的模型及插值方法, 不同的方法插值结果差别很大, 即便是同一种插值方法, 在不同的研究区域得到的插值结果也会不同[3, 12]。如何根据一个区域的地形、气候特征与站点数据选择最适合当地的插值方法, 对于降水量空间化是一个值得探讨和研究的问题[11]。
目前, 对于新疆地区降水的空间插值研究较少, 且未形成有效的方法和成果。何等[12]基于新疆地区18个基本气象站点基于反距离加权法和克里格方法对新疆降水量进行了插值, 王智等[6]采用确定性函数和地统计学的综合插值方法进行新疆地区年降水量的空间插值与比较验证分析, 仲嘉亮[5]采用了反距离加权法、径向基函数法和克里格法的方法对降水量插值精度进行比较研究。然而, 所有的研究结果都未对新疆周边国家的气象站点作为插值数据, 并且没有把目前国内外应用最广泛的ANUSPLIN软件作为对比对象[1, 9, 13, 14]。鉴于此, 本研究利用新疆地区及周边地区和国家的154个气象站点降水数据进行空间插值, 选用最常用的反距离权重法(IDW)、普通克里金法(Kriging)、协同克里格法(Cokriging)、贝叶斯法(EBK)和ANUSPLIN软件5种插值方法[1, 14]对新疆地区10年的降水进行空间插值, 并对插值结果进行验证, 分析5种插值方法的特点, 以期找出适合新疆地区降水量空间插值方法, 为研究降水变化、植被与降水之间的关系, 制作草原综合顺序类型图等提供可靠的降水空间信息。
本研究使用了1995-2004年新疆地区及其周边的地区和国家的154个气象台站月降水数据, 其中, 新疆周边国家的台站数据来源于美国NOAA的国家环境信息中心网站(http://www.ncdc.noaa.gov/ghcnm/v3.php), 新疆地区及新疆周边地区的台站数据来自中国气象科学数据共享服务网(http://cdc.cma.gov.cn/)。由于插值的边缘效应, 本研究选择的插值范围比新疆地区的实际范围大, 为70.7° -99.2° E, 31.3° -51.4° N。
数字高程数据来源于SRTM网站(http://srtm.csi.cgiar.org/), 为SRTM-DEM Version 4数据。该数据空间分辨率为90 m, 数据格式为Geo-Tiff。150个气象站的空间分布如图1所示。
空间插值是运用已知的空间样本数据对未知的地理空间特征进行评估[15]。本研究选择5种常用的插值方法:1)IDW法以样本点与插值点间的距离作为权重, 并对权重进行加权平均处理, 样本点距离插值点越近, 则赋予的权重越大, 样本点距离插值点越远, 则赋予的权重越小[1, 10]。2)Kriging是在地质统计学中以结构性分析和半变异函数理论作为基础, 在一定的区域内对变量进行最优无偏估算的一种数学方法, 对研究具有结构性与随机性的空间分布变量有独特的优点[11]。3)Cokriging法与Kriging法的基本原理相同, 但其考虑变量最少为1个以上, 通过交叉变异函数模型或交叉协方差函数的建立, 用于易控制和观测的变量对未知的变量进行局部估算[5]。4)ANUSPLIN软件法。Craven和Wahba[16]在1978年提出了薄盘平滑样条表明拟合技术, 是使用薄盘平滑样条方法对多变量数据进行内插的工具。ANUSPLIN软件法是薄盘光滑样条法的拓展[17], 通过引进多种协变量子模型, 同时进行多个表面的气象空间插值, 如海岸线与降水距离之间的关系。5)EBK法是由托马斯· 贝叶斯首次提出的[18], EBK法可有效构建克里金模块中较困难的阶段, 其他的克里金插值方法需要手动调试一些参数来得到准确的结果, 它可通过自动构建子集和模拟过程来计算这些参数[1]。
本研究采用交叉验证法对5种插值方法的精度进行评价, 该方法首先假定所有的气象台站数据未知, 通过对周围已测台站数据进行空间估算, 最后测算实测值与估计值的差值, 交叉验证法可准确地评价不同空间插值方法的相对精度[6, 10, 19]。本研究采用平均绝对误差(mean absolute error, MAE), 均方根误差(root mean squared error, RMSE)和平均相对误差(mean relative error, MRE)作为5种插值方法的评价指标。
MAE=
MRE=
RMSE=
式中:Zx和Zy分别代表降水量实测值和预测值; n为测站数。
本研究通过两种途径比较5种插值结果。第1种是把根据插值的MAE、MRE和RMSE作为一个判断标准。第2种是把插值结果与已建立的新疆的降水量分布格局进行比较, 新疆降水空间分布与新疆的地形地貌特征有很大的关系。天山以北(北疆)降水较多, 天山以南(南疆)降水较少, 西多东少, 山区降水较多, 平原区降水较少, 降水的多少与地形地貌分布关系密切。就北疆来说, 天山北坡和阿尔泰山降水较多, 准噶尔盆地降水较少。南疆的天山南坡和昆仑山降水较多, 但明显低于天山山区和阿尔泰山山区, 塔里木盆地降水最少[20, 21]。
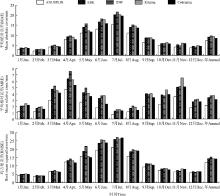
通过交叉验证对5种方法插值的MAE、MRE和RMSE的对比分析(图2), 结果表明, 年降水量的MAE排序为ANUSPLIN< Cokriging< EBK< Kriging< IDW, 其值依次为7.29、8.63、9.21、9.35和9.72 mm。MRE和RMSE的排序与MAE的排序基本一致, MRE的值分别为2.17、3.11、3.43、3.73和3.74; RMSE的值分别为12.14、14.09、14.46、14.42和15.37 mm。5种插值方法的MAE、MRE和RMSE的变化都有明显的季节性, MAE和RMSE表现为秋冬两季低于春夏两季, 1月到7月, MAE和RMSE的值逐渐升高, 7月到12月呈现下降趋势。MRE的月变化与MAE和RMSE不太一致, MRE的值在春季和秋季较高。利用MAE、MRE和RMSE作为评价标准对5种插值方法分析得知, 5种插值方法在新疆地区均得到精度较高的降水空间信息, MAE和RMSE表现为秋冬两季误差低于春夏两季, MRE在春季和秋季较高。总的来看, 通过ANUSPLIN软件的降水插值结果精度最高。
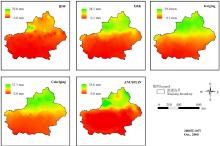
鉴于1995-2004年的月平均的插值图较多, 本研究仅选取有代表性的2000年1月、4月、7月和10月的降水量进行对比分析。2000年1月的5种方法的插值结果显示:IDW法明显受到气象站点的影响, 新疆地区降水量较大的区域主要位于天山西段, 伊犁地区可达50 mm, 这明显高于其他4种方法的插值结果(图3)。Kriging插值结果与IDW相比, 降水的空间分布有一定的改变, 但是降水较大区域从准噶尔盆地延续到塔里木盆地边缘, 这明显跟实际不相符。EBK、Cokriging和ANUSPLIN的插值结果很相似, 但Cokriging的插值结果分布不太均匀, EBK和ANUSPLIN得到的插值结果分布较为均匀, 插值得到的空间降水未出现异常值, 低值区与高值区的空间分布与当地情况基本一致, 空间插值结果较好。
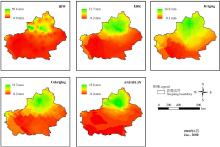
从2000年4月插值结果看出(图4), Kriging法和Cokriging法的插值结果相似, 降水主要分布在天山南坡以南的区域; EBK法和IDW法的插值结果相似, 降水主要分布在天山西段和阿尔泰山; ANUSPLIN软件插值的降水主要分布在天山中西段、阿尔泰山和昆仑山, 其中塔里木盆地和准噶尔盆地降水较少, 该方法得到的新疆地区4月空间降水未出现异常值, 在空间分布上符合新疆地区的实际情况, 空间插值结果较好。
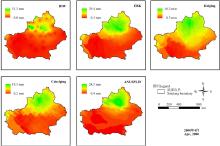
5种方法对7月份降水结果显示(图5), IDW和Kriging的插值结果明显受到台站的影响, EBK和Cokriging法插值结果均质性较差, 且在塔里木盆地东端有较高的降水量, 这明显与现实不太相符, ANUSPLIN插值主要分布于天山西段、阿尔泰山山脉和昆仑山山脉, 塔里木盆地和准噶尔盆地降水较少, 降水量随高程变化而变化。
从10月的插值结果看出(图6), 同1月、4月、7月一样, IDW的插值结果明显受到台站的影响, 其他4种插值方法的降水插值空间分布格局类似, 降水主要分布在天山以北, 但是EBK和Cokriging插值结果不连续。
总之, 5种插值方法在一定程度上能反映新疆降水的空间分布特征, 但在1月、4月、7月和10月表现各有差异, 相对来说, ANUSPLIN软件插值结果优于其他4种插值方法。
 | 图3 5种插值方法对新疆地区2000年1月份降水的插值表面Fig. 3 Precipitation interpolation surface from five interpolation methods for Xinjiang region in January 2000 |
 | 图4 5种插值方法对新疆地区2000年4月份降水的插值表面Fig. 4 Precipitation interpolation surface from five interpolation methods for Xinjiang region in April 2000 |
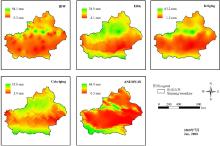 | 图5 5种插值方法对新疆地区2000年7月份降水的插值表面Fig. 5 Precipitation interpolation surface from five interpolation methods for Xinjiang region in July 2000 |
5种插值方法在新疆地区不同月份的MAE、MRE和RMSE的变化明显不同, 这主要与新疆地区不同月份的降水量和降水形式不同有关, 在新疆地区降水主要集中在4月-9月, 且主要以降水量的形式出现, 而10月到翌年3月的降水较少, 且主要以降雪的形式出现[22, 23]。这导致了降水较多的月份的MAE和RMSE较大, 而在降水较多月份的MAE和RMSE较小。这与三江源[14]和陇西祖厉河流域[24]降水量四季分布的研究结果一致, 在降水量较多的季节的MRE值较小, 这与在东北地区[25]的研究结果一致。不管是三江源地区、还是陇西祖厉河流域和东北地区, 其季节降水分布与新疆地区都较为相似。
在新疆地区, 利用5种插值方法在1月、4月、7月和10月的误差分析可知, 年降水量的MAE排序为ANUSPLIN< Cokriging< EBK< Kriging< IDW, MRE和RMSE的排序与MAE的基本排序一致, 其中, ANUSPLIN方法的插值精度都明显优于其他4种方法, ANUSPLIN方法在西南复杂山地[26]也比较适合。
IDW法的最大值或者最小值主要分布在台站周围, 与实际情况相差较远, 受气象站分布的影响非常明显, 其原因主要是新疆气象台站稀少, 特别是南疆和东疆地区, 空间分布极不均匀, 台站主要分布在塔里木盆地和准噶尔盆地的周边区域, 两个盆地中心和阿尔泰山、天山和昆仑山都没有台站。Kriging法在10月插值效果较好外, 在其他的3个月插值效果依然不好。由于考虑了海拔因素, Cokriging法插值误差较Kriging法有一定的改进, 但新疆地区的气象站点海拔相对较低, 并不能完全反映“ 高程” 信息, 在空间结构上仍然没有取得理想的插值结果。Cokriging法插值结果均质性较差, 并不能反映新疆实际降水的空间分布。EBK法在降水较多的4月和7月插值与实际偏差较大, 而在降水较少的1月和10月插值效果较好, 因此, 在降水较少的1月和10月可选择EBK法。ANUSPLIN软件不但能考虑地形因子及海岸线距离的影响, 其插值结果更精细, 精度更高, 兼顾了插值曲面的准确度与平滑度, 它较为正确地反映了新疆地区降水空间分布的特征, 而且操作方便, 插值效率高, 需手动调节的参数较少, 从而减少了插值的不确定性因素。因此, 在新疆地区降水量空间化首选ANUSPLIN软件。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|